
recall, that the value of
L
∗
(
n
)
corresponds to the maximum size of
reversible circuit from all minimal circuits, implementing even permutation
h
∈
A
(
Z
n
2
)
using additional inputs.
Theorem 4
.
Given
N
∼
5
∙
2
n
/n
additional inputs in the circuit,
composed of gates from
Ω
2
n
+
N
set,
L
∗
(
n
)
.
2
n
+1
is true.
J
Let us show, that
L
∗
(
h
)
.
2
n
+1
for all
h
∈
A
(
Z
n
2
)
. Any
h
∈
A
(
Z
n
2
)
permutation defines some Boolean transformation
f
h
:
Z
n
2
→
Z
n
2
. It will be
represented in the following form:
f
h
(
h
x
1
, . . . , x
n
i
) =
=
⊕
a
1
,...,a
k
∈
Z
2
x
a
1
1
∧
. . .
∧
x
a
k
k
∧
f
h
(
h
a
1
, . . . , a
k
, x
k
+1
, . . . , x
n
i
)
.
(10)
The
f
h
(
h
a
1
, . . . , a
k
, x
k
+1
, . . . , x
n
i
)
transformation corresponds to some
Boolean transformation of
n
−
k
variables.
Let us construct a multi-terminal circuit, calculating all Boolean
functions of
n
−
k
variables. We will denote by
Ω
NXA
a set of gates
{¬
,
⊕
,
∧}
(NXA – NOT, XOR, AND). The
Ω
NXA
set is the functionally
complete basis. It is known that no more than
2
2
n
−
k
gates from
Ω
NXA
set is required to construct the multi-terminal circuit described above.
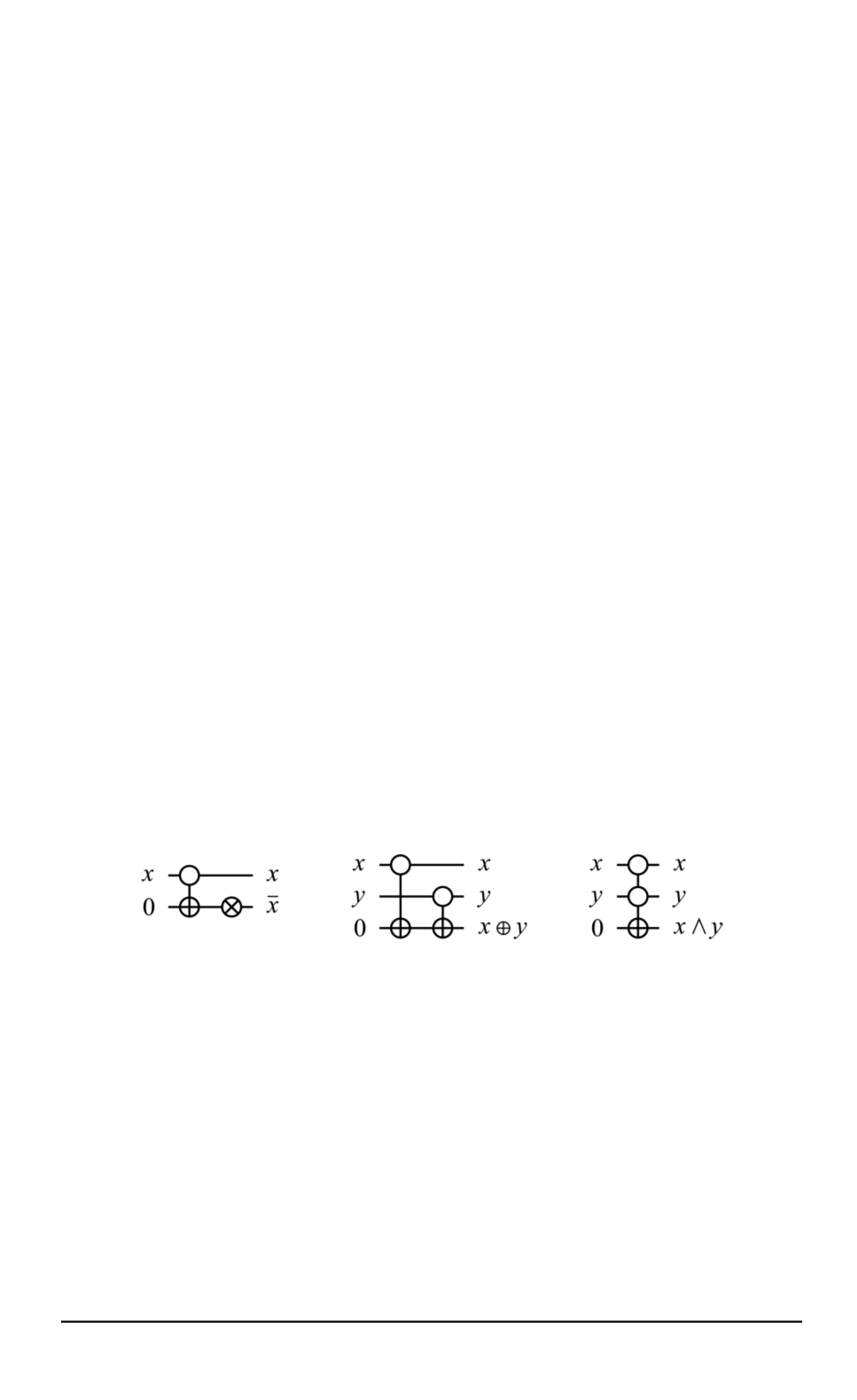
All these gates can be represented as a composition of NOT, CNOT and
2-CNOT reversible gates. According to the figure below, no more than
two reversible gates and no more than one additional input are required.
Therefore, reversible sub-circuit defining described above multi-terminal
circuit has the size of
L
1
6
2
2
n
−
k
+1
and it uses
N
1
= 2
2
n
−
k
−
(
n
−
k
)
additional inputs. Every output that corresponds to one of the additional
inputs is an output of the
n
−
k
variable Boolean functions.
Representing functional elements from
Ω
NXA
basis as a composition of NOT, CNOT
and 2-CNOT reversible gates
Before calculating all possible values of
x
a
1
1
∧
. . .
∧
x
a
k
k
we will calculate
all
ˉ
x
i
,
1
6
i
6
k
inversions with reversible gates. To do this
L
2
= 2
k
NOT
and CNOT gates and
N
2
=
k
additional inputs are needed. Then we
calculate all possible values of
x
a
1
1
∧
. . .
∧
x
a
k
k
by induction: for one input,
for two etc. To do this
L
3
=
k
−
1
X
i
=1
2
i
+1
= 2
k
+1
−
4
2-CNOT gates and
N
3
=
L
3
additional inputs are needed.
Then we construct a sub-circuit to calculate
f
h
transform. For each
vector
h
a
1
, . . . , a
k
i
L
4
=
n
2-CNOT gates are needed to define a conjunction
78 ISSN 0236-3933. HERALD of the BMSTU. Series “Instrument Engineering”. 2015. No. 1

















