
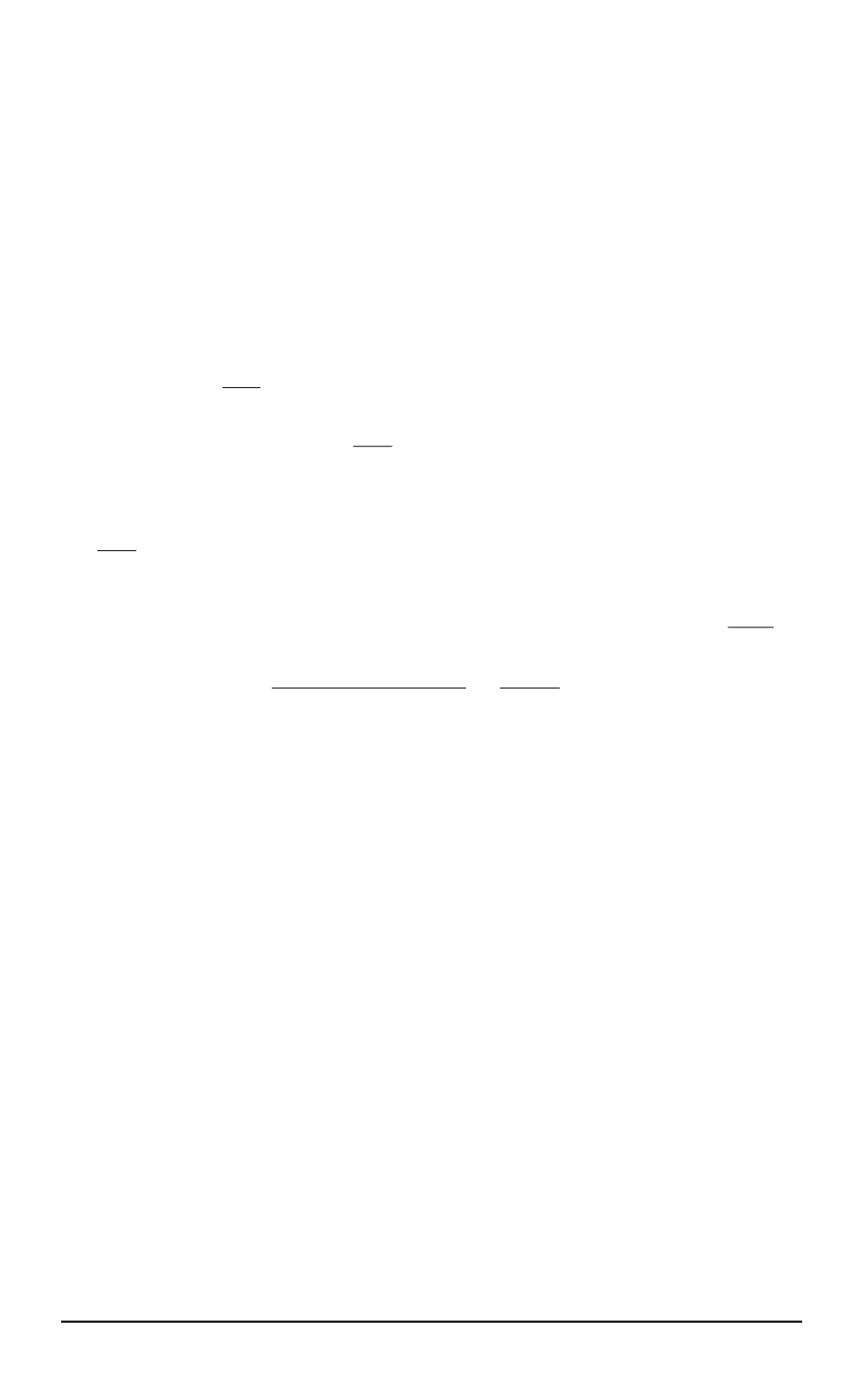
L
(
g
(
K
)
)
6
5
X
i
=1
L
i
;
L
(
g
(
K
)
)
6
2
n
+ 2
k
+1
+ (
k
−
1)(2
k
+1
+ 40 log
2
k
)+
+2(
n
−
log
2
k
) + 8(
n
−
log
2
k
−
3)
.
Reducing this formula, we will obtain
L
(
g
(
K
)
)
6
12
n
+
k
(2
k
+1
+
+40 log
2
k
)
−
50 log
2
k
−
24
. Given
K
= 2
the inequation
L
(
g
(2)
)
6
12
n
+
+ 324
is true.
Let us substitute calculated estimations into formula (7):
L
(
h
)
.
2
n
k/
2
(12
n
+
k
(2
k
+1
+ 40 log
2
k
))) +
k
(12
n
+ 324);
L
(
h
)
.
2
n
+1
12
n
k
+ 2
k
+1
+
o
(
k
) +
O
(
kn
)
.
Given
k
=
o
(
n
)
the estimation of
L
(
h
)
can be reduced:
L
(
h
)
.
2
n
+1
×
×
(
12
n
k
+ 2
k
+1
)
.
Let
m
= log
2
n
−
log
2
log
2
n
. The proof required
k
to be the power of
two. Let
k
= 2
log
2
m
, then
m/
2
6
k
6
m
and
L
(
h
)
.
2
n
+1
12
n
m/
2
+
+2
m
+1
= 2
n
+1
24
n
log
2
n
−
log
2
log
2
n
+
2
n
log
2
n
. Therefore
L
(
h
)
.
.
52
n
2
n
/
log
2
n
for all
h
∈
A
(
Z
n
2
)
. Hence,
L
(
n
)
.
52
n
2
n
/
log
2
n
.
I
Corollary.
Given
k
= 4
the
L
(
n
)
.
6
n
2
n
relation is true, which is
asymptotically less than estimation
(3)
, given in work
[7]
.
Combining the lower and upper bounds
L
(
n
)
it is possible to formulate
the main theorem of this work.
Theorem 3.
L
(
n
)
n
2
n
/
log
2
J
Results from theorems 1 and 2.
I
Reducing gate complexity, using additional inputs.
In work [3] it was
proved that for any Boolean transformation
f
:
Z
n
2
→
Z
n
2
it is possible to
construct the implementing circuit composed of gates on
{¬
,
∧
,
∨}
basis,
with
O
(2
m
/m
)
gate complexity, where
m
=
n
+ log
2
n
. Such a circuit
includes a multi-terminal circuit as a sub-circuit, computing all Boolean
functions of
n
−
k
variables. In order to prove the following representation
of
f
transformation was used (equivalent to Boolean function expansion
for
k
variables):
f
(
h
x
1
, . . . , x
n
i
) =
⊕
a
1
,...,a
k
∈
Z
2
x
a
1
1
∧
. . .
∧
x
a
k
k
∧
f
(
h
a
1
, . . . , a
k
, x
k
+1
, . . . , x
n
i
)
.
Using the same approach we will prove that the upper bound of
reversible circuits can be reduced by using additional inputs. Let us
ISSN 0236-3933. HERALD of the BMSTU. Series “Instrument Engineering”. 2015. No. 1 77

















